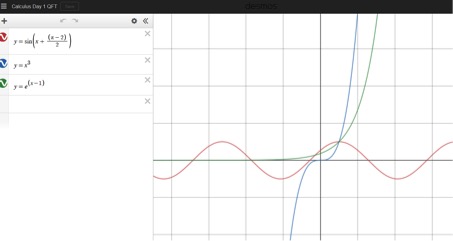
Since Massachusetts starts the school year later than most of the country, I wanted to jump straight into the action on day one.
Someone in my AP Calculus Facebook group posted these graphs and described what he did with them on his first day of class. (This person attended a workshop led by Dennis Donovan, a fellow Massachusetts teacher and co-author of Barron’s AP Calculus. I want to give big thanks and credit to both of them.)
I combined his activity with what I learned from the Right Question Institute. It turned out to be one of the best first days I’ve ever had.
Here’s what I did.
On the very first day, I took attendance and put up the following graphs from my Desmos file (Desmos is an online graphing tool.)
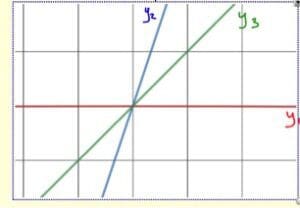
My seniors in AP and honors calculus were already very familiar with the Question Formulation Technique (QFT) process from their science classes, so we zipped right through.
They worked in groups, and even though all the honors groups came up with similar priority questions, what I got from them was an amazing discussion!
The following were the groups’ priority questions:
What are the equations of the lines?
What’s the intersection point?
What is the relationship between the lines?
What is the point of intersection?
What type of equations are the lines?
Is there a hole?
What does it represent?
Where are the axes relative to the lines?
What are the equations of the lines?
Why are the lines at different angles?
What is the relationship between the lines?
Why isn’t the graph numbered?
What’s important about where they intersect?
What are the equations of the lines?
Where are the axes?
What’s the intersection point?
Do the lines represent something?
Are they ever undefined?
At first, I was a little surprised none of the honors groups asked what this picture had to do with calculus. But, that’s why we do this, right? They were much more focused on what information they were not given. One group did want to know if the behavior of each line stayed the same and if there was more of the graph they couldn’t see. But, for whatever reason, they did not choose either as a priority question. Each group presented their questions, and I just let them talk to each other about what they were wondering.
Here are their other (non-priority) questions:
Why are the lines different colors?
What are the values of the other points?
Does have significance?
Where are the axes?
Is the point of intersection the origin?
Are they lines or segments?
What is the slope of each line?
Do they have a common variable?
Are the lines logarithmic?
Does y = 0 for line 1?
Do the subscripts have to do with the line are they just names?
Is there a reason for these lines?
Why are they different colors?
How are the ys related?
What do the numbers do/represent?
Why do they all intersect at the same point?
Do they intersect at 0?
What is their relationship?
Why are the slopes different? Why isn’t it in a graph form?
What are the differences between the lines?
Why are they numbered?
Why do they all pass through the same point?
Why are they lettered “y”?
What is this representing?
What is the slope of the blue one?
Why do they intersect?
What’s the scale?
Is the red at zero?
Is the intersection the point of origin?
Do the 3 lines have any kind of relationship?
What does each quadrant represent?
What’s the slope?
Relative to the lines, where is the x,y axis?
Do they all use the same variable?
I did this activity three times that day. Here are the questions from the AP Calculus groups:
What are the equations of the lines?
Do they continue their linear behavior?
Do they have any other zeros?
What are the equations of the lines?
What is the window of the graph?
Do the lines represent something?
How do the lines relate to calculus?
What does the intersection represent?
Where is the origin?
What is the scale?
Are there any discontinuities as the graph goes on?
Is that a 3D plane?
Why are they all labeled ‘y’?
How does this relate to calculus?
What I found interesting was that some of the questions the honors kids asked were very basic — more so than I thought they would be. The AP kids asked some basic questions mixed in with some higher-level questions using better vocabulary.
I also let the AP Calculus kids bounce their questions off each other for a while.
When each class was done wrapping up their questions, I zoomed out, gradually, so they could see what was really going on. The honors kids were amused, and the AP kids went nuts!
In each class, I talked about the concept of local linearity and instantaneous rate of change. The kids were used to studying functions on a big scale: zeros, end behavior, relative extrema, domain, and range. I explained that we would now be focusing on what’s happening to our dependent values as we get very, very close to a certain independent value. All three classes had experience with limits from their Algebra 2 classes, but it didn’t occur to them to use this information.
The QFT allowed my students to hit the ground running on the first day of class. They could discuss mathematical information without any fear. Students could get their brains going, be engaged, and walk out feeling good about their new math class. For me, I can never go back to taking attendance and reading the course expectation sheet again. This was the most rewarding first day in 30 years.