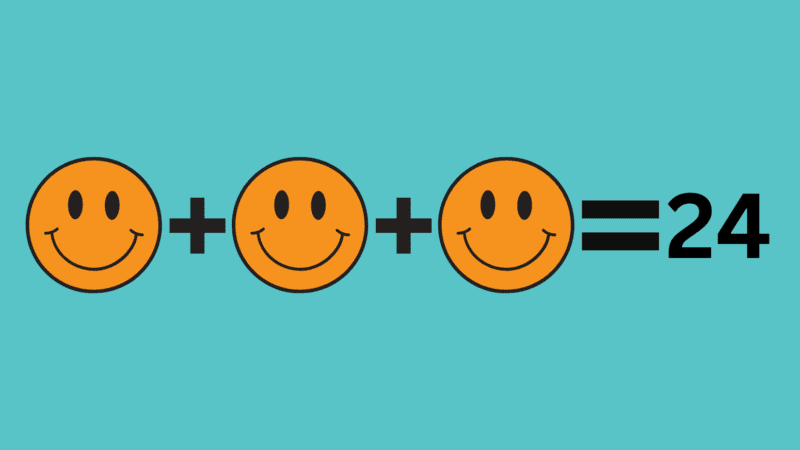Finding Question Focus prompts to use for a QFT in English or social studies might seem on the surface to be easier than finding them for math. Many teachers pull an interesting quote from a book, use an essay prompt, or share a curious primary source. However, there are many creative and engaging prompts you can craft from your curriculum to spark questions and promote math learning.
Earlier this year, as part of the National Council for Math Teachers (NCTM) virtual conference, RQI staff member Katy Connolly and high school math teacher Tracy Brown teamed up to present a short, pre-recorded workshop about using the QFT to bring curiosity and joy to math learning. Selecting examples of how the QFT has been applied in math classrooms in preparation for this conference inspired us to think more deeply about what goes into designing a math Question Focus, or QFocus.
Here are four ideas for creating your own math QFocus prompt, inspired by examples from math teachers that we pulled out of the archives.
Idea 1: Combine mathematical elements with non-mathematical elements
Teachers have shown time and again that the QFT can work well in math. In fact, one of the very first QFT examples we often share with teachers is a math example. Deirdre Brotherson, a fourth-grade teacher in Hooksett, New Hampshire, used the following prompt at the start of a unit on variables, the goal being to understand what the students did and didn’t already know about the topic:
🙂+ 🙂+ 🙂= 24
Brotherson received a range of responses from students, everything from, “What do the smiley faces mean?” to, “Can we replace each smiley face with an 8?” and, “Do the numbers have to be the same because the smiley faces are the same?” While some students clearly approached the topic with more prior knowledge than others, all students were able to engage in some way with the prompt.
What worked about this QFocus is that it combined the familiar with the unfamiliar. It used something students recognized (a smiley face symbol) with a concept they didn’t yet understand — variables, or by definition, “symbols that represent a mathematical object.” Teachers often attest that new math concepts can be daunting for some students, especially if they are concerned that their lack of background or inability to pick something up “quickly” sets them behind other students. The fear of looking unknowledgeable in front of peers can prevent students from speaking up or participating at all.
In this lesson, for students who had never worked with variables, the smiley faces in the prompt gave them something to anchor on to. For those who already knew how variables worked, the unsolved equation gave them a window to start speculating about solutions.
Another example of how to combine mathematical elements with non-mathematical elements comes from George Marenco, a high school algebra teacher from Sacramento, California. He used the Question Focus “Equations = Balance” to prompt students to develop essential questions about a unit on equations. Students wondered, “What is Balance in math?” “How do we find balance?” “How do I know if it starts off balanced?” and “Why does an equation have to be balanced?” George notes that “the answers to those questions prompted a discussion about the differences between expressions and equations [and] laid a wonderful foundation for later discussions about inequalities”, all helping to guide students’ investigations throughout the unit.
Idea 2: Use a word problem or other exam question as the QFocus
In a second math QFT, Deirdre Brotherson tried something new for the QFocus: a word problem. This was a multiple choice word problem that came straight out of preparatory materials for state testing:

Asking questions first, rather than immediately diving into to solve the problem, required Brotherson’s fifth-grade students to slow down and clarify what was being asked, and what they needed to know first. This turned out to be essential. Their initial questions revealed confusion about the vocabulary being used in the problem: “What does ‘down’ mean?” “What is a discount?” After pausing to learn the vocabulary, students were better prepared to think about the process of solving, and the second round of questions looked like: “Do we cross out +30 problems?” “Do we do 110+30 first?” and, “If we do 110+30 that is the amount he put down and the discount, right?”
Idea 3: Have students do some work on a math problem first, and then ask questions about the results
One way to make the most of a math QFT is to give some pre-work ahead of the QFocus, so that students are already warmed up and thinking through the topic before asking and working with their questions.
Often, the experience of working through a math problem can provoke more and deeper questions than just thinking about the topic in the abstract. As Rick Barlow, a high school algebra teacher in San Jose, California, found, students’ QFT questions were even more focused on quadratics after they had a hands-on encounter with the concept.
Taking inspiration from Dan Meyer’s 3 Act Math Tasks, Barlow started the lesson by giving students a leading question: “How many bingo chips can fit in a 22 x 22 square?” Students first attempted to answer that question by experimenting with real bingo chips, using several squares of different sizes, and collecting their data in a chart. Once student groups had their completed chart on hand, the Question Focus was presented to them: “The function that best models this data.”
The resulting questions demonstrated students drawing from their prior math knowledge to figure out what to do next with the data they had collected: “What would you call a function that is neither linear or exponential?” “What would the slope look like?” “How can you find what the table is multiplying by?” and, “Is this related to polynomial?” Barlow then used selected questions as opening slides for the following day’s lesson, showing students how the questions they asked, and were most curious about, were directly connected to what they would be learning about that day in class.

Meanwhile, Claire Yablong, an algebra teacher in Phoenix, had a similar idea for her QFocus. Her class was also working on quadratic functions, although they’d already learned some of the material. She decided to do the QFT to understand why the class performed poorly on a quiz. What were they not understanding?
Like Barlow, she also had students do some pre-work to set up the Question Focus. Students were given an equation 3X2 – 5X=12 and had two opportunities to try solving it: first individually, and then with a partner, using a different method each time. Then, students got into groups of four and started the QFT. They asked lots of questions like: “How do you factor with two X’s?” “Do you have to move the 12 over before you start every time?” “How do you know when to stop?” “Why do we set the equation equal to zero?” “Why are there two answers?” and, “How would you know what is the best method to use on a question by question basis?” Yablong noted afterward: “I think our QFT day forced some of them to stop saying ‘I don’t get this’ and instead get specific about what they didn’t understand.”
Alternatively, you might show students a problem that has already been worked out, which is what George Marenco does. Like previous examples, “students find their own entry point to interact with the math”, he says, “but having the problem worked out for them limits potential discouragement because students don’t feel like they have to get an answer.”
Idea 4: Use “real-world” statistics, data, or primary sources
Finally, for students who find it difficult to connect what they’re learning in math class to the so-called “real-world,” pulling a statistical graph, some powerful data, or a primary source for your QFocus might be the key to piquing their interest in the subject. Primary sources aren’t just for social studies!
Gloria Mitchell, an eighth-grade teacher in Berwyn, Illinois, wanted to use the unique mathematics involved in counting votes for presidential elections as a concrete real-life application for a unit on data analysis. She decided to use a primary source as the QFocus: a famous 1948 photograph of President Truman holding a newspaper with the headline “Dewey Defeats Truman” alongside her statements, “The newspaper headline in this image is about a presidential campaign. There has never been a President Dewey.” Students started asking if the headline was referencing a primary election, or if maybe it was a misprint. Their questions sparked an excited class discussion as they investigated the math — statistical sampling errors — that caused the pollsters to make the wrong call.

Tracy Brown from Orangeburg, South Carolina, also saw an opportunity to use primary sources as QFocuses in her Algebra 1 course. She used historical maps showing differences between the electoral vote and the popular vote in the 1700s and 1800s, and the same comparison (electoral v. popular) in the 2000s. After students worked to understand the differences in these maps through their questions, they eventually constructed their own scatter plot graphs to visually represent the size of the rift between popular vote and the electoral college over the years. The Library of Congress has a whole curated set of interesting historical charts and graphs that could be used to prompt questions from students about how math has been historically used to display information, visualize data, inform decisions, communicate with the public, and more.
Alternatively, modern day examples of math in daily life can be great content for a QFocus. Take for example this picture of Macy’s coupons. One teacher used it to spark questions and discussion about percentages. Students immediately wanted to know which of the coupons was a better discount for shoppers. Gloria Mitchell also suggests checking out the New York Times series called “What’s Going on in this Graph?” , which posts a new fascinating graph every week and invites students to discuss them. What else around us every day could inspire questions and math connections?

For more inspiration, explore our collection of classroom examples of the QFT in math. Or, begin by looking closer to home. Where do you see opportunities to craft a QFocus out of your existing curriculum materials?